Statistics and Probability (Time, Tables, & Diagrams)
Vad vi kommer jobba med:
Centralt innehåll
Plausibility assessments when estimating and making calculations in everyday situations.
Comparing, estimating and measuring length, area, volume, mass, time and angles using common units of measurement. Measurements using contemporary and older methods.
Tables and diagrams to describe the results of investigations. Interpretation of data in tables and diagrams.
Graphs for expressing different types of proportional relationships in simple investigations.
Strategies for mathematical problem-solving in everyday situations
Mathematical formulation of questions based on everyday situations.
Förmågor
Kunskapskrav
Centrala begrepp
Centrala frågeställningar
| Kunskapskrav för betyget E i slutet av årskurs 6 | Kunskapskrav för betyget C i slutet av årskurs 6 | Kunskapskrav för betyget A i slutet av årskurs 6 | |
|---|---|---|---|
| Kriterie | Eleven kan lösa enkla problem i elevnära situationer på ett i huvudsak fungerande sätt genom att välja och använda strategier och metoder med viss anpassning till problemets karaktär. Eleven beskriver tillvägagångssätt på ett i huvudsak fungerande sätt och för enkla och till viss del underbyggda resonemang om resultatens rimlighet i förhållande till problemsituationen samt kan bidra till att ge något förslag på alternativt tillvägagångssätt. | Eleven kan lösa enkla problem i elevnära situationer på ett relativt väl fungerande sätt genom att välja och använda strategier och metoder med förhållandevis god anpassning till problemets karaktär. Eleven beskriver tillvägagångssätt på ett relativt väl fungerande sätt och för utvecklade och relativt väl underbyggda resonemang om resultatens rimlighet i förhållande till problemsituationen samt kan ge något förslag på alternativt tillvägagångssätt. | Eleven kan lösa enkla problem i elevnära situationer på ett väl fungerande sätt genom att välja och använda strategier och metoder med god anpassning till problemets karaktär. Eleven beskriver tillvägagångssätt på ett väl fungerande sätt och för välutvecklade och väl underbyggda resonemang om resultatens rimlighet i förhållande till problemsituationen samt kan ge förslag på alternativa tillvägagångssätt. |
| Kriterie | Eleven har grundläggande kunskaper om matematiska begrepp och visar det genom att använda dem i välkända sammanhang på ett i huvudsak fungerande sätt. Eleven kan även beskriva olika begrepp med hjälp av matematiska uttrycksformer på ett i huvudsak fungerande sätt. I beskrivningarna kan eleven växla mellan olika uttrycksformer samt föra enkla resonemang kring hur begreppen relaterar till varandra. | Eleven har goda kunskaper om matematiska begrepp och visar det genom att använda dem i bekanta sammanhang på ett relativt väl fungerande sätt. Eleven kan även beskriva olika begrepp med hjälp av matematiska uttrycksformer på ett relativt väl fungerande sätt. I beskrivningarna kan eleven växla mellan olika uttrycksformer samt föra utvecklade resonemang kring hur begreppen relaterar till varandra. | Eleven har mycket goda kunskaper om matematiska begrepp och visar det genom att använda dem i nya sammanhang på ett väl fungerande sätt. Eleven kan även beskriva olika begrepp med hjälp av matematiska uttrycksformer på ett väl fungerande sätt. I beskrivningarna kan eleven växla mellan olika uttrycksformer samt föra välutvecklade resonemang kring hur begreppen relaterar till varandra. |
| Kriterie | Eleven kan välja och använda i huvudsak fungerande matematiska metoder med viss anpassning till sammanhanget för att göra enkla beräkningar och lösa enkla rutinuppgifter inom aritmetik, algebra, geometri, sannolikhet, statistik samt samband och förändring med tillfredsställande resultat. | Eleven kan välja och använda ändamålsenliga matematiska metoder med relativt god anpassning till sammanhanget för att göra enkla beräkningar och lösa enkla rutinuppgifter inom aritmetik, algebra, geometri, sannolikhet, statistik samt samband och förändring med gott resultat. | Eleven kan välja och använda ändamålsenliga och effektiva matematiska metoder med god anpassning till sammanhanget för att göra enkla beräkningar och lösa enkla rutinuppgifter inom aritmetik, algebra, geometri, sannolikhet, statistik samt samband och förändring med mycket gott resultat. |
| Kriterie | Eleven kan redogöra för och samtala om tillvägagångssätt på ett i huvudsak fungerande sätt och använder då bilder, symboler, tabeller, grafer och andra matematiska uttrycksformer med viss anpassning till sammanhanget. I redovisningar och samtal kan eleven föra och följa matematiska resonemang genom att ställa frågor och framföra och bemöta matematiska argument på ett sätt som till viss del för resonemangen framåt. | Eleven kan redogöra för och samtala om tillvägagångssätt på ett ändamålsenligt sätt och använder då bilder, symboler, tabeller, grafer och andra matematiska uttrycksformer med förhållandevis god anpassning till sammanhanget. I redovisningar och samtal kan eleven föra och följa matematiska resonemang genom att ställa frågor och framföra och bemöta matematiska argument på ett sätt som för resonemangen framåt. | Eleven kan redogöra för och samtala om tillvägagångssätt på ett ändamålsenligt och effektivt sätt och använder då bilder, symboler, tabeller, grafer och andra matematiska uttrycksformer med god anpassning till sammanhanget. I redovisningar och samtal kan eleven föra och följa matematiska resonemang genom att ställa frågor och framföra och bemöta matematiska argument på ett sätt som för resonemangen framåt och fördjupar eller breddar dem. |
Inte publicerad än
Inte publicerad än
Week 2: Lesson 3: Project Presentations
Complete Oral Presentations from last term: Operation Vacation
Week 3: Lesson 1: Reading Analog and Digital Time
What is time?
Week 3: Lesson 2: Elapsed Time
elapsed time = how much time has passed.
Week 3: Lesson 3: +/- Time and Units of Time
Adding and subtracting time
Week 4: Lesson 1: Reading Tables
What are timetables used for? Where do we see timetables?
Week 4: Lesson 2: Reading Tables and Planning a Journey
In this lesson, students will examine a timetable, which includes arrival and departure times. They will need to determine lengths of time as well as applying the table to real-life situations.
Week 4: Lesson 3: Reading Tables and Calculating Time
In this lesson, students will use timetables to calculate journey lengths. They will continue to practise adding and subtracting time, as well as examining elapsed time.
Week 5: Lesson 1: Frequency Tables & Bar Charts
Key Terms:
survey - to ask (many people) a question or a series of questions in order to gather information about what most people do or think about something (när man undersöker vad folk tycker.)
streck (tally mark) - a way of keeping track of numbers in groups of 5. In surveys, a tally mark represents an answer from one single person.
frekvens (frequence) - how many tally marks a particular category has.
- We record tally marks in a frequency table when we do a survey.
Week 5: Lesson 2: Line Graphs
Review the features of bar charts and graphs: STOLAR: scale, title, origin (zero), labels, arrows, ruler
Week 5: Lesson 3: Pie Charts
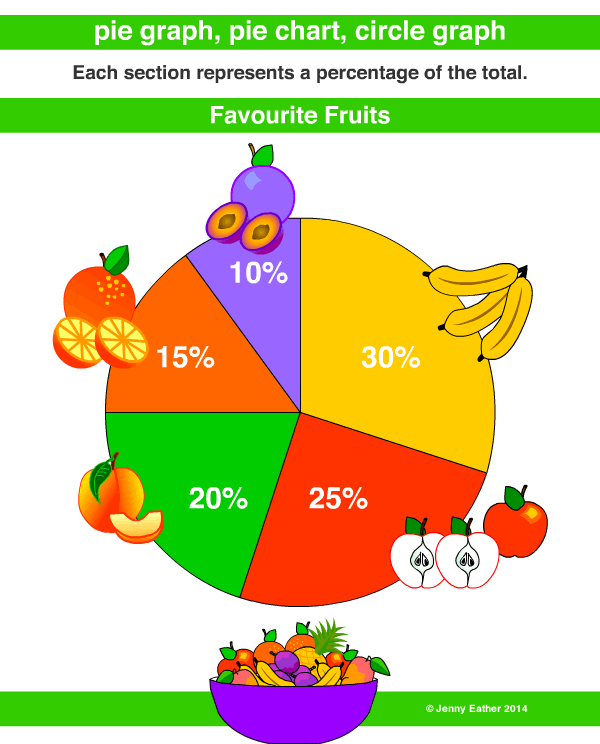
Pie chart: a type of graph in which a circle is divided into sectors that each represent a proportion of the whole. The whole of the circle is equal to 100%.
Week 6: Lesson 1: Review of Graphs
Today we will review the different types of graphs we have been working with.
Week 6: Lesson 1: Averages & Range
This week, we will be discussing how to find different types of averages from a set of data.
- Mean - Medelvärde (add all the numbers and divide by the amount of elements/numbers in total)
- Median - Median (the number in the middle of a set of numbers listed in ascending order)
- Mode - Typvärde (the number that appears the most often (has the highest frequency) in a set of data (numbers)
Week 6: Lesson 2: Averages & Range
Week 7: Lesson 1: Checkpoint Review
In this lesson, we will review all of the topics covered so far this term, in order to prepare for next lesson's checkpoint.
Problems from Class
Averages & Range
a) 2, 1, 1, 5, 6
b) 2, 7, 4, 2, 3, 6, 11
c) 24, 31, 12, 38, 12, 15
Time
1. The time is 14:05. What will the time be in 5 hours and 25 minutes?
2. Lisa’s dance class ended at 18:20. If the class was 1 hour and 30 minutes long, when did it start?
3. Billy visited Disneyland with his family. They got to the park at 09:50 and left at 17:35.
How much time did they spend at Disneyland?
Billy’s cousin Lily joined them at the park at 11:15. She left the park at the same time as Billy. How much longer was Billy at the park than Lily?
Line Graph
Jennifer just started a Youtube channel. She uploaded her first video yesterday and checked how many view she was getting each hour. She recorded the views in the table below.
10:00 - 7
11:00 - 9
12:00 - 5
13:00 - 12
14:00 - 14
15:00 - 19
Make a line graph showing this information.
Pie Chart
Draw this pie chart on the board: 50% Thailand, 25% Spain, 12,5% Greece, 12,5% Italy.
What fraction of the students wanted to visit Spain for vacation?
What fraction of students wanted to visit Greece for vacation?
What percentage of students chose Thailand or Spain?
If 24 there are 24 students in the class, how many voted for Thailand? How many for Spain?
Week 7: Lesson 2: Checkpoint
Week 7: Lesson 3: Checkpoint Review
In this lesson, we will discuss the answers to the checkpoint and continue to review for next week's assessment.